[Design] BST Node Insertion / Deletion

First Word

For BST it’s very important to do insert and delete (balancing not required).

Insertion is easy, but deletion is very difficult. However, it’s a good idea to at least know the principles.

Insert a node

Steps:

1. check whether new value = current node value. If not, proceed.

2. if new value is less, than:

   1. if current node has no left child, set left to new value, and return

   2. otherwise, go to left child and start over

3. if new value is greater, than:

   1. if current node has no right child, set right to new value

   2. otherwise, go to right child and start over

Note:

The BST may not be balanced after the insertion.

Code

Code snippet from this article

public boolean add(TreeNode node, int value) {
	if (value == node.val)
		return false;
	if (value < node.val) {
		if (node.left == null) {
			node.left = new TreeNode(value);
			return true;
		} else {
			return add(node.left, value);
		}
	} else if (value > node.val) {
		if (node.right == null) {
			node.right = new TreeNode(value);
			return true;
		} else {
			return add(node.right, value);
		}
	}
	return false;
}

Delete a node

Steps:

1. Find the node
2. Find the maximum node in the left subtree
3. Replace the node with the maximum node in the left subtree.

Special Cases:

1. The node doest have a left child.
2. The maximum node in the left subtree has a left child.
3. The node is the root of the tree

Code

The source code given by ninechap

private void myDeleteNode(TreeNode parent, TreeNode node) {
	if (node.left == null) {
		if (parent.right == node) {
			parent.right = node.right;
		} else {
			parent.left = node.right;
		}
	} else {
		TreeNode maxNodeParent = node;
		TreeNode maxNode = node.left;

		// find the maximum node in the left sub tree
		while (maxNode.right != null) {
			maxNodeParent = maxNode;
			maxNode = maxNode.right;
		}

		if (maxNodeParent.left == maxNode) {
			maxNodeParent.left = maxNode.left;
		} else {
			maxNodeParent.right = maxNode.left;
		}

		// move replacedNode to node
		maxNode.left = node.left;
		maxNode.right = node.right;
		if (parent.left == node) {
			parent.left = maxNode;
		} else {
			parent.right = maxNode;
		}
	}
}

private void findAndDelete(TreeNode parent, TreeNode node, int val) {
	if (node == null) {
		return;
	}
	if (node.val == val) {
		myDeleteNode(parent, node);
	} else if (node.val < val) {
		findAndDelete(node, node.right, val);
	} else {
		findAndDelete(node, node.left, val);
	}
}

public TreeNode deleteNode(TreeNode root, int val) {
	TreeNode dummyNode = new TreeNode(0);
	dummyNode.left = root;
	findAndDelete(dummyNode, root, val);
	return dummyNode.left;
}

A little bit on balancing

There are 2 ways to balance a tree. Most common method is tree rotation:

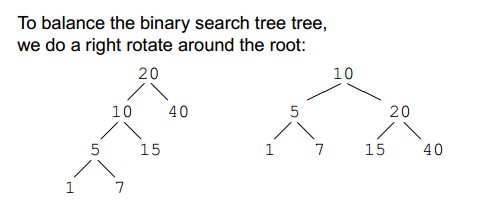
An AVL Trees means a self-balancing search trees. If balance gets out of range −1…+1, the subtree is rotated to bring into balance.

Second way is to convert tree into a linkedlist, then build the tree again (we have discussed this algorithm before, pick the middle element).

This method is slow if we insert and re-balance on each step, but we can do bulk insert/delete forgetting about the re-balancing for a while. This will make the data structure faster! more details