Question List
- Liar truth-teller (skip)
- Toggler brain teaser
- Alien abduction
- Blue forehead room
- Forehead numbers
- Light bulb switching
- Path counting (skip)
- 3D path counting
Toggler brain teaser
“你前面站了 5 个人,他们中间只有一个人讲真话……”
这个问题比上个问题难就难在,你只知道他们五个中有一个只讲真话,但其余四个,他们有时候讲真话,有时候讲假话,只有一点可以确定,这四个人将真话和假话有个规律:如果这次讲了真话,下次就会讲假话,如果这次讲假话,下次就讲真话。你的任务是,把五个人中那个只讲真话的人找出来。
你可以问两个问题,两个问题可以向同一个人发问,也可以分别问两个人。
你该问什么问题?
小提示:你可以这样安排两个问题承担的任务:首先你可以先问一个问题,不管得到的答案是什么,你都能从中知道下一个问题你将得到的答案是真是假。
求职者的最佳答案:
随便找一个人,首先问:“你是那个只讲真话的吗?”如果答案是肯定的,你再问这个人:“谁是只讲真话的?”;如果第一个问题你得到的答案是否定的,你就再问对方“谁不是只讲真话的?”
正如这个问题给出的提示,第一个问题的价值在于,如果你得到的答案是“我是”,那么你问的人要么是那个只讲真话的,要么是那个这一轮讲假话的“半真话半假话”者,不管是谁,他下一轮一定会说真话。所以你可以继续问这个人:“谁是只讲真话的?”对方的答案就是正确答案。
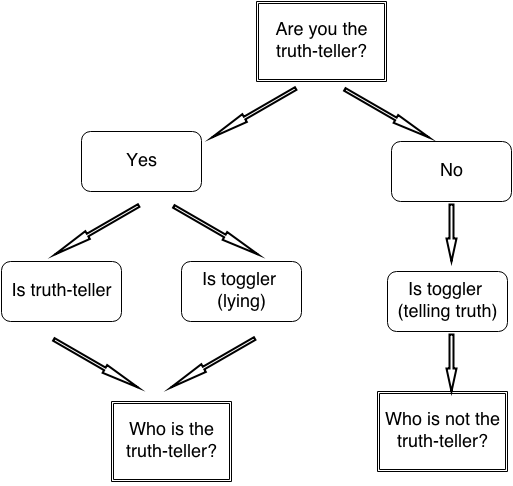
如果对第一个问题你得到的答案是“我不是”,那么回答者不可能是只讲真话的那个人,只能是一个此轮讲真话的“半真话半假话”者。此人下一轮将会说假话,所以你应该问他:“谁不是只讲真话的?”同样他告诉你的,只能是那个只讲真话的。
Alien abduction
“外星人打算将地球用来种蘑菇,并且已经抓了十个人类……”
外星人用这十个人代表地球 60 亿人口,将通过外星人的方式来测试这十个人,决定地球是不是有资格加入跨星际委员会,如果没有,就把地球变成一个蘑菇农场。
明天,这十个人将被关在一间漆黑的屋子里前后排成一队,外星人将给每个人戴一顶帽子,帽子为紫色或者绿色,然后外星人会将灯打开,这十个人每个人都无法看见自己头上的帽子是什么颜色,但可以看见排在你前面的每个人头上帽子的颜色。
帽子的颜色是随机的,可能全是紫的,也可能全是绿的,或者是任意的组合。
外星人会从后往前问每一个人:“你头上的帽子是什么颜色?”如果这个人答对了,这个人就安然无事,他所代表的地球上 6 亿人口也将获救。否则,这个人将被爆头,外星人将把他所代表的 6 亿人口变成蘑菇的肥料。每个人的答案屋子里所有人都可以听到。
现在,人类的命运在你手上,你可以设计一个方案,使这十个人提前制定一个计划,这个计划必须拯救尽可能多的人。
提示:有个方案可以让你拯救其中至少九个人。
求职者的最佳答案:
第十个人计算排在前面的所有人的绿帽子是奇数还是偶数并向前面的人发出一个信号,这样排在前面人就可以再通过排在更前面的所有人的绿帽子的奇偶数是否变化来判断自己帽子的颜色,因为如果绿帽子奇偶发生变化,那自己就是那个导致变化的“绿帽子”,如果没变化,自己就是“紫帽子”。
因为所有的人除了回答外星人的问题不能说话,所以第十个人的“信号”只能包含在自己的答案里,比如如果排在前面的九个人有奇数顶绿帽子,这个人类就告诉外星人自己的帽子是“绿色”,如果是偶数,就猜自己的帽子是“紫色”。这样等于给他前面的人一个暗号,排在他前面的这个人,可以通过计算自己前面的所有人的绿帽子的奇偶变化来判断自己的帽子是绿还是紫。
排在最后的那个人为了大众利益没有选择,根据前面的人的帽子情况告诉外星人自己是“绿帽子”还是“紫帽子”,他的答案有 1/2 的几率正确,但他前面的人一定都能答对。
还没懂?比如第十个人看到前面有奇数个绿帽子,他就告诉外星人自己的是绿色,这是他前面的人就知道他的意思是前面九个人中有奇数个绿帽子,这是第九个人再数前面八个人的,如果前面八个人中也有奇数个,那自己就是紫色帽子。第九个人告诉外星人自己是紫色帽子,第八个人就知道绿帽子没有减少还是奇数个,再数数前面七个人绿帽子数的奇偶,就可以判断自己帽子的颜色;反之,如果第九个人告诉外星人自己是绿色帽子,那第八个人就应该知道绿色帽子减少了一个由奇数变成了偶数,再看看前面所有的绿帽子情况作出判断。这样一个接一个,只要每个人都认真听后面的人的答案并在心里计算所剩绿帽子的奇偶变化,前面九个人都能获救。
当然,你也可以计算紫色帽子的奇偶。
Blue forehead room
“100 个完美的逻辑学家坐在一个房间里……”
这是一个电视真人秀节目,节目里 100 个拥有完美无瑕逻辑思维能力的人围成一圈坐在一个房间里。在进入房间前,这 100 个人被告知,100 个人中至少有一个人的额头是蓝色的。你可以看见别人额头的颜色,但无法看到自己的,你需要对自己额头是不是蓝色进行猜测,在房间的灯被关掉时,如果你推测出你的额头是蓝色的,你需要站起来离开房间。
然后房间的灯被再次打开,那些认为自己额头是蓝色的人已经不在屋内。接下来灯会再次被关掉,剩下的人中推测自己额头是蓝色的离开房间,如此重复。
问题来了,假设这 100 个人的额头都是蓝色的,将会发生什么情况?注意,这 100 个人都有完美无瑕的逻辑推理能力,他们会根据其他人的额头颜色对自己进行合理的推理和猜测。
提示:想想看,如果 100 个人不全是蓝色额头,又会发生什么情况?
求职者的最佳答案:
将会出现的情况是:灯关了又开,开了又关,重复到第一百次时,所有人都同时离开。
这是为什么呢?想想看,每个人都看见其他 99 个人额头是蓝色的,灯关掉后再打开,发现这 99 个蓝色额头的同伴都没有离开,然后灯再次关掉后打开,如此重复 100 遍后,所有人同时离开了房间。
这么理解吧,假设只有一个人的额头是蓝色的,由于这 100 个人事先被告知至少有一个人额头是蓝色,所以这个人如果看到其他 99 个人额头都不是蓝色,立马就知道自己是蓝色,所以灯一关掉,这个人就会离开房间。
如果有两个人额头是蓝色呢?
其中一个蓝色额头的人会想:我的额头可能是蓝色也可能不是蓝色,现在其他 99 个人中有一个蓝色额头的人,如果我不是蓝色,那么就只有这一个人是,那么他看到我们都不是蓝色额头就能推断出他是,那么灯一关他就会离开,我先等一下,灯再打开如果他已经走了,那就证明我的额头不是蓝色的。
反之,如果我的额头是蓝色的,那个蓝色额头的人的想法会和我刚才的想法一样先等一等,第一次关灯他不会离开,这样如果灯开了那个蓝色额头的人还在,就证明我的额头也是蓝色的。这样第二次关灯我们俩会一起离开。
以此类推,如果有三个人额头是蓝色,你看到另外两个人额头是蓝色,应该推算出如果自己的额头不是蓝色的话,那么灯第二次关的时候他们俩会同时离开,如果他们俩没有同时离开,那就证明我的额头是蓝色的,我应该在第三次关灯的时候离开。结果是,三个蓝色额头的人在第三次关灯的时候同时离开。
把上述逻辑重复一百遍,你就得到了最上面的正确答案。
Forehead numbers
“逻辑学家们围成一圈坐着,他们的额头上面画有数字……”
又来一个逻辑学家围成一圈的问题,这次是这样的,三个拥有完美逻辑推理能力的人围成一圈坐在一个房间里,每个人的额头上都画着一个大于 0 的数字,三个人的数字各不相同,每个人都看得见其他两个人的数字,看不见自己的。
这三个数字的情况是,其中一个数字是其他两个数字的和,已知的情况还有,其中一个逻辑学家的数字是 20,一个是 30。
游戏组织者从这三个逻辑学家后面走过,并问三个人各自额头上的数字是什么。但第一轮每个逻辑学家都回答他们无法推测自己的数字是什么。游戏组织者只好进行第二轮的发问,这是为什么?你能据此猜出三个逻辑学家的数字吗?
求职者的最佳答案:
结果由第三个逻辑学家的答案而定。他们三个的数字分别是 20,30 和 50。
假设第二个和第三个逻辑学家额头上的数字是 20 和 30,这时候如果第一个逻辑学家的数字是 10,那么第二个逻辑学家看到其他两个人一个是 10,一个是 30,会想:“我要么是 20,要么是 40。”
第三个逻辑学家看到其他两个人一个是 10,一个是 20,会想:“我要么是 30,要么是 10,但我不会是 10,因为每个数字都不一样,所以我应该是 30。”
这样第三个逻辑学家就会猜出自己的数字是 30 了,但他没有,第一轮谁也没有准确推测出自己的数字,这说明我们的前提不正确,第一个逻辑学家的数字不是 10,那么他只能是 50。
Light bulb switching
“你面前有一百个灯泡,排成一排……”
一百个灯泡排成一排,第一轮你把他们全都打开亮着,然后第二轮,你每隔一个灯泡关掉一个,这样所有排在偶数的灯泡都被关掉了。
然后第三轮,你每隔两个灯泡,将开着的灯泡关掉,关掉的灯泡打开(也就是说将所有排在 3 的倍数的灯泡的开关状态改变)。
以此类推,你将所有排在 4 的倍数的灯泡的开关状态改变,然后将排在 5 的倍数的灯泡开关状态改变……
第 100 轮的时候,还有几盏灯泡亮着?
提示:如果你是第 n 轮(n 大于 1 小于 100),排在 n 的倍数位置的灯泡的开关状态就发生转变。
反过来,比如第 8 个灯泡,当你在 8 的因子轮(即第 1,2,4 和 8 轮)的时候,它就会改变开关状态。所以对于第 m 个灯泡,如果 m 有奇数个因子,你的开关状态就发生奇数次变化。
求职者的最佳答案:
10 盏灯泡亮着,这 10 盏灯泡排位数都是平方数。
根据提示已经可以看出,这个问题的实质就是找出有多少个灯泡的排位数拥有奇数个因子。每拥有一个因子,到这个因子数的那一轮时,这个灯泡就会被转换开关状态。
比如第 1 轮,因为所有 100 个数字都有因数 1,所以全部被打开;第 2 轮,只有那些拥有 2 这个因子、能被 2 整除的数字的灯泡转换状态被关掉;第 3 轮,只有那些拥有 3 这个因子、能被 3 整除的数字的灯泡被转换状态。以此类推,如果灯泡排位数拥有奇数个因子,意味着它被打开和关上奇数次,那它就最终还是被打开的状态,如果灯泡排位数拥有偶数个因子,那它最终就是被关上的状态。
比如第 1 个灯泡有奇数个因子,第 2 个有偶数个(1,2),第 3 个有偶数个(1,3)第 4 个有奇数个(1,2,4),所以 第 4 个灯泡最后还是亮着的。
最终计算得出,所有排位数为平方数的灯泡最终还是亮着的,因为这些数都拥有奇数个因子,1,4,9,16……
在 100 以内,共有 10 个平方数,分别是 1,4,9,16,25,36,49,64,81,100。这 10 个排位数的灯泡,最终都还是亮着。
3D path counting (most difficult)
“你有一个立方体,立方体的边长是 3……”
这个问题比前面那个从左上格子走到右下格子的问题难,因为那毕竟是个平面问题。如图所示,这次的任务是从立方体的背面左上的小立方体走到完全相对的正面右下小立方体。
你可以往上移,也可以往下移,还可以往前移。You can movetoward the front, you can move down, or you can move upward。
问题还是,你共有几种走法?
求职者的最佳答案:
90 种,思路是将这个立方体分成“三层”。
上面平面图的那道题的思路就是个最好的提示。你可以将这个立方体分成“三层”,粉红色代表最上面那层,紫色代表中间那层,橘红色代表下面那层。
现在,我们把问题变成了:从左边、右边和上边到达目标小立方体的走法共有多少(如图所示,即到达紫色中间层最右下脚方块以及橘红色最右下脚左边以及上边相邻方块的方法)?假设从起点小立方体到达终点小立方体左边相邻小立方体共有 m 种方法,到达右边相邻小立方体共有 n 种方法,到达上边相邻小立方体有 r 种方法,那我们需要求出来的,就是 n+m+r。
按照前面那道平面题的思路和方法,你就可以一点一点计算出来我们的正确答案。
| 1 | 1 | 1 |
|---|---|---|
| 1 | 2 | 3 |
| 1 | 3 | 6 |
Layer 1
| 1 | 2 | 3 |
|---|---|---|
| 2 | 6 | 12 |
| 3 | 12 | 30 |
Layer 2
| 1 | 3 | 6 |
|---|---|---|
| 3 | 12 | 30 |
| 6 | 30 | 90 |
Layer 3
A better and more elegant mathamatics solution is available here