Question
Find Nth fibonacci number in O(logN) time complexity.
Solution
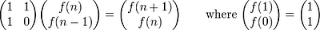
It’s a recursive sequence, where we can get the following equation:
A* [ F(1) F(0) ] = [ F(2) F(1) ]
A* [ F(2) F(1) ] = [ F(3) F(2) ] = A^2 * [ F(1) F(0) ]
A* [ F(3) F(2) ] = [ F(4) F(3) ] = A^3 * [ F(1) F(0) ]
..
..
..
..
A* [ F(n) F(n-1) ] = [ F(n+1) F(n) ] = A^n * [ F(1) F(0) ]
Which means:
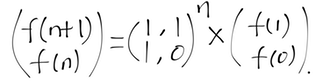
So all that is left is finding the nth power of the matrix A. Well, this can be computed in O(log n) time, by recursive doubling. For more, see question post or here.
Code
not written