Question
有一个 n*m(n 和 m 都不超过 50)的棋盘,有 k 个目标格子需要访问。需要访问的格子的横纵坐标存放在数组 x[]和 y[]中(0<=x[i]<n, 0<=y[i]<m)。
遍历的规则为:
每一步只能从一个目标格子水平或者竖直跳跃移动到另一个目标格子。
连续的两步必须形成直角。即如果前一步是水平移动,那么下一步只能竖直移动。
问是否存在一种遍历顺序,使得每个目标格子有且仅被访问一次。
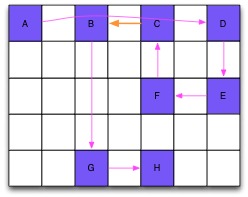
样例:k=8, x=[0, 0, 0, 0, 2, 2, 4, 4], y=[0, 2, 4, 6, 4, 6, 2, 4],对应于下图中 A, B, C, D, F, E, G, H 8 个目标格子,存在满足条件的遍历 A->D->E->F->C->B->G->H。
Solution
n,m 的棋盘,建一个包含 n+m 个顶点的图 G(为了方便说明,类似二分图将其分为两列,左边 n 个顶点,右边 m 个顶点,分别代表 n 行和 n 列)。
对于目标格子(i,j),左边第 i 个顶点和右边第 j 个顶点连一条边。最后的问题其实就是问转换之后的图 G 是否存在欧拉欧拉回路或者欧拉路径。