[Question] Check if two line segments intersect

Question

link

Given two line segments (p1, q1) and (p2, q2), check if 2 line segments intersect.

Orientation

Considering 3 pointer, orientation can be:

1. counterclockwise
2. clockwise
3. colinear (not considering direction)

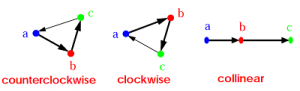
Note that orientation only tells the order and sequence relationship of 3 points. It tells nothing about intersection.

Intersection

Considering 2 line segments: (p1,q1) and (p2,q2).

Case 1: general

Two line segment intersect if BOTH the 2 conditions hold:

1. (p1, q1, p2) and (p1, q1, q2) have different orientations and
2. (p2, q2, p1) and (p2, q2, q1) have different orientations

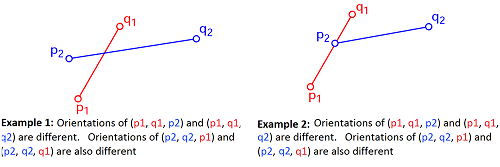
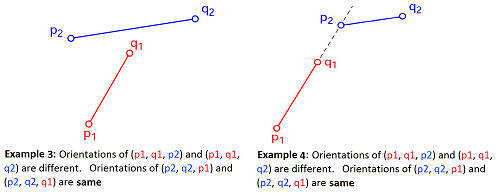
Case 2: special

The speical case is: what if all 4 pointers (p1, q1, p2, q2) are all on the same line!!! Well, this definitely can happen.

If so, check if the values of x-axis and y-axis intersect. I.e. the below 2 cases:

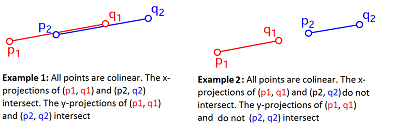
Code

Translated from G4G:

public boolean intersect(Pair p1, Pair q1, Pair p2, Pair q2) {

	int o1 = orientation(p1, q1, p2);
	int o2 = orientation(p1, q1, q2);
	int o3 = orientation(p2, q2, p1);
	int o4 = orientation(p2, q2, q1);

	// General case
	if (o1 != o2 && o3 != o4) {
		// 2 lines intersect
		return true;
	}

	// Special Cases
	Segment seg1 = new Segment(p1, q1);
	Segment seg2 = new Segment(p2, q2);

	// p1, q1 and p2 are colinear and p2 lies on segment p1q1
	if (o1 == 0 && onSegment(seg1, p2))
		return true;

	// p1, q1 and p2 are colinear and q2 lies on segment p1q1
	if (o2 == 0 && onSegment(seg1, q2))
		return true;

	// p2, q2 and p1 are colinear and p1 lies on segment p2q2
	if (o3 == 0 && onSegment(seg2, p1))
		return true;

	// p2, q2 and q1 are colinear and q1 lies on segment p2q2
	if (o4 == 0 && onSegment(seg2, q1))
		return true;

	return false; // Doesn't fall in any of the above cases
}

private boolean onSegment(Segment seg, Pair q) {
	// check if q lies on line segment seg(p1, p2)
	if (q.x <= Math.max(seg.p1.x, seg.p2.x)
			&& q.x >= Math.min(seg.p1.x, seg.p2.x)
			&& q.y <= Math.max(seg.p1.y, seg.p2.y)
			&& q.y >= Math.min(seg.p1.y, seg.p2.y))
		return true;

	return false;
}

private int orientation(Pair first, Pair second, Pair third) {
	int val = (second.y - first.y) * (third.x - second.x)
			- (second.x - first.x) * (third.y - second.y);
	if (val == 0) {
		// colinear
		return 0;
	} else {
		// clock or counterclock wise (1 or -1)
		return val / Math.abs(val);
	}
}

class Segment {
	Pair p1;
	Pair p2;

	public Segment(Pair p1, Pair p2) {
		this.p1 = p1;
		this.p2 = p2;
	}
}